Desafios com Números Irracionais

Associe V ou F às afirmativas:

I - A soma de dois números irracionais poderá ser um número racional.

II - O produto de dois números irracionais poderá ser número racional.

III - A razão de dois números racionais poderá ser um número inteiro.

A sequência que representa a referida associação é:

a) V - F - V

b) F - V - V

c) V - V - V

d) V - F - F

e)V-V-F

Por: LuanSales               

  http://www.matematica.com.br/site/index.php?option=com_content&view=article&id=585:matematica-basica&catid=53:desafios&Itemid=197

números irracionais

Foi só em 1872 que o matemático alemão Dedekind (1831-1916) fez entrar na Aritmética, em termos rigorosos os números irracionais que a geometria sugerira há mais de vinte séculos.

Racional - número que se pode escrever da forma h/k, onde h e k são inteiros com    k¹ 0.

Irracional – número que não se pode expressar como quociente de dois números inteiros.

Exemplos de números irracionais

Todas as raízes quadradas de números naturais que não sejam quadrados perfeitos, isto é se a raiz quadrada de um número natural não for inteira, é irracional.

Logo são irracionais Ö 2, Ö 3, Ö 5, Ö 7, Ö 8, Ö 10,Ö n , com n natural e n ¹ de um quadrado perfeito

Números representáveis por dízimas infinitas não periódicas.

São irracionais os resultados da soma, subtracção, multiplicação e divisão de um número irracional com um número racional.

Ex: 1 + Ö 3, (1 + Ö 5)/2, (Ö 8 – 1)/2

São igualmente irracionais          

Não são irracionais   

São irracionais  os números especiais f,  p , e.

Reunindo o conjunto dos números irracionais ao conjunto Q dos racionais, obtemos o conjunto R dos números reais.

N Í N₀ Í ZÍ Q Í R

Em R permanecem válidas todas as propriedades e regras do cálculo estabelecidas para as operações em Q.

 http://www.educ.fc.ul.pt/icm/icm99/icm17/numirra.htm

  O IRRACIONAL ø

    ø =1,6180339887... ou ø =(1 + sqr(5))/2 é considerado símbolo de harmonia. Os artistas gregos usavam-no em arquitetura; Leonardo da Vinci, nos seus trabalhos artísticos; e, no mundo moderno, o arquiteto Le Corbusier, com base nele, apresentou, em 1948, O modulor. O número de ouro descobre-se em relações métricas:

- na natureza: em animais (como na concha do Nautilus) flores, frutos, na disposição dos ramos de certas árvores;
- em figuras geométricas, tais como o retângulo de ouro, hexágono e decágono regulares e poliedros regulares;
- em inúmeros monumentos, desde a Pirâmide de Quéops até diversas catedrais, na escultura, pintura e até na música.

Leticia

A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritemética. Os de natureza geométrica podem ser ilustrados com o problema da medida da diagonal do quadrado quando a comparamos com o seu lado.

  

Leticia

Foi só em 1872 que o matemático alemão Dedekind (1831-1916) fez entrar na Aritmética, em termos rigorosos os números irracionais que a geometria sugerira há mais de vinte séculos. De facto a origem histórica da necessidade de criação dos números irracionais está  ligada com dados de geométricos que se podem concretizar no  problema da medida da diagonal do quadrado quando a comparada com o seu lado. De facto já na época de Pitágoras o problema tinha surgido:   

De facto pelo Teorema de Pitágoras: " A soma dos quadrados dos catetos é igual ao quadrado da hipótenusa " Neste quadrado, de lado 1, verificamos que  d² = 1² + 1² = 2,  então teremos que o comprimento da diagonal é dado pela 2.

Leticia

Um dos métodos de solução é isolar, em um dos membros da equação, os termos que incluem raízes, e elevar ambos os membros a uma mesma potência que elimine a raiz. No entanto, este procedimento não produz uma equação equivalente a original, mas sim uma equação que possui entre as suas soluções os valores que resolvem a equação inicial.
Por exemplo, quando se tem a igualdade entre uma certa expressão x e outra expressão y, pode-se concluir que x² = y². Por outro lado, é perfeitamente possível que duas expressões tenham os quadrados iguais, sem que elas próprias sejam iguais. Este é o caso, por exemplo, quando se tem , pois para a maioria dos números, (a igualdade só vale para x = 0). Assim, se durante a resolução ambos os membros forem elevados a uma certa potência, será necessário chegar se os valores obtidos como solução para a nova equação são também soluções da equação inicial.
Acompanhe o próximo exemplo:

Isolando a raiz, elevando ao quadrado e resolvendo:

                         

Leticia

Uma equação irracional é uma equação onde existem polinômios e raízes.
Por exemplo:

Uma definição mais precisa seria: uma equação algébrica irracional é uma equação onde existem funções racionais e inversas de funções polinomiais.



Leticia

Ludolph van Ceulen

Ludolph van Ceulen foi um matemático alemão que empreendeu mais de trinta anos da sua vida aperfeiçoando o método de cálculo do número irracional de Pi (π). O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe Jamshid Masud Al-Kashi com 16 casas decimais. Ludolph van Ceulen, no final do século XVI, calculou em 1596 um valor de π com 35 casas decimais. O número foi 3.14159265358979323846264338327950288.

Sabrina

Historia do números Irracionais

Os números irracionais são números que não se podem exprimir como uma razão (isto é, um quociente, uma fracção) de números inteiros. São… incalculáveis e incomensuráveis. Por isso também lhe chamaram números “mudos”, números“cegos”, números “surdos”, ou ainda números que “perderam a razão”…

A origem histórica da necessidade de criação dos números irracionais está  ligada com dados de geométricos que se podem concretizar no  problema da medida da diagonal do quadrado quando a comparada com o seu lado:

Teorema de Pitágoras:  " A soma dos quadrados dos catetos é igual ao quadrado da hipótenusa "  Dado um quadrado de lado igual à unidade, quanto mede a diagonal? Neste quadrado, de lado 1, verificamos que a diagonal  d² = 1² + 1² = 2,  então teremos que o comprimento da diagonal é dado pela √2.

 Foi a tentar resolver este problema usando o Teorema de Pitágoras que os gregos descobriram um "novo" número: o número √2.

O Teorema de Pitágoras provocou, assim, a descoberta de novos números: os irracionais. Representam um marco importante para o pensamento humano, mas foi muito perturbadora para os pitagóricos. De tal maneira, que quiseram manter secreta esta descoberta.

A raiz quadrada de 2 é portanto um dos números irracionais mais célebres. Se tentarmos calculá-la vemos logo que deve ser 1 e …. Qualquer coisa. Mas a “qualquer coisa” é que é o problema! Alguns matemáticos antigos iam perdendo também a razão a tentar descobrir essa “qualquer coisa”! O mais que apuraram, pobres deles, foi 17/12, que é 1 mais “qualquer coisa” (1 é, como sabes, 12/12). Mas o quadrado de 17/12 é 289/144… E que 2 é… 288/144!

Era “quase”!

Os números irracionais são números que são quase exprimíveis como um quociente de números inteiros… Mas a que falta sempre o “quase”!

Assim,

Um número será irracional quando não se pode traduzir por uma fracção do tipo a/b. Dito de outra maneira: Um número diz-se irracional quando não pode exprimir-se por uma dízima finita ou infinita periódica. (Uma dízima será infinita periódica quando existir um conjunto de algarismos que se repete. Exemplo: 1,23452345... que muitas vezes se escreve 1,(2345). O período é o conjunto  desses algarismos que se repetem, no nosso exemplo o período é 2245)

 De: Luan Sales

http://sites.google.com/site/susymcmarques/historiadosnumerosirracionais     

Hipaso de Metaponto

Hípaso de Metaponto foi um filósofo membro da Escola Pitagórica. Nasceu em torno do ano 500 a.C. em Metaponto, cidade grega da Magna Grécia situada no  Golfo de Tarento, ao sul do que agora é a Itália.

Se crê que foi quem provou primeiramente a existência dos números irracionais, em um momento em que os pitagóricos pensavam que os números racionais podiam descrever toda a geometria do mundo. Hípaso de Metaponto havia quebrado a regra de silêncio dos pitagóricos, revelando ao mundo a existência destos novos números. Isso havia feito com que estes o expulsassem da escola e erigissem uma tumba com seu nome, mostrando asssim que, para eles, ele estava morto.

Os documentos da época dão versões diferentes de seu final. Uns dizem que morreu em um naufrágio de circunstâncias misteriosas; outros, que se suicidou como autocastigo, dando, assim, liberdade a sua alma para buscar a purificação em outro corpo; dizem ainda que um grupo de pitagóricos o matou, normalmente na descrição, afogado, e há inclusive a teoria que diz que Pitágoras em pessoa o condenou à morte.

Supõe-se que sua demonstração, por métodos geométricos, envolvia que a hipotenusa de um triângulo isósceles com catetos de comprimento igual a uma unidade, i.e. raiz quadrada de dois (constante de Pitágoras), não poderia ser expressa pela razão entre números inteiros.

Sabrina

Fonte: http://pt.wikipedia.org/wiki/Hipaso_de_Metaponto

Frases.. Sobre Matematica.

Toda a educação científica que não se inicia com a Matemática é, naturalmente, imperfeita na sua base.

Auguste Conté

“(...)Se nós vivêssemos sem a Matemática, isso fazia com que fossemos regularmente enganados pelos outros(...)”

Nuno Miguel de Sousa Barreira         

11ºA  Escola Sec. Figueiró dos Vinhos 1997

Os pontos não têm partes nem dimensões.

   Como podem combinar-se para formar uma linha?

                                                                 J. A. Lindon

 

A Matemática não é algo mágico e ameaçadoramente estranho, mas sim um corpo de conhecimento naturalmente desenvolvido por pessoas durante um período de 5000 anos ...

Frank Swetz

Fonte:  http://www.prof2000.pt/users/folhalcino/activmat/frasemat.htm

DayaneRocha.

Pi ( π )

Japonês afirma ter recalculado a constante matemática PI e chegado a 5 trilhões de decimais – quase o dobro do recorde anterior.

A façanha foi feita por Shigeru Kondo em parceria com o americano Alexander Yee, que desenvolveu o programa de computador necessário para os cálculos

Segundo informações da AFP, o número ainda está sujeito a verificações para que se possa constatar se o recorde do francês Fabrice Bellard foi batido. Em janeiro deste ano, ele calculou o PI com 2,7 trilhões de dígitos – um número tão grande que ocupa mais de um terabyte de espaço para ser armazenado e levaria 49 mil anos para ser falado em voz alta.

O PI é a mais antiga constante matemática conhecida, já estudada na Grécia Antiga. Ele representa a razão entre a circunferência de qualquer círculo e seu diâmetro. Na escola, usamos seu valor aproximado para cálculos simples (3,14), porém o número é usado em incontáveis situações – da engenharia à ciência da computação.

Antes do francês Bellard, outro japonês havia estabelecido o recorde, em agosto de 2009. Utilizando um supercomputador, um cientista da Universidade de Tsubaka fez os cálculos em apenas 29 horas

Sabrina.

Fonte: http://olhardigital.uol.com.br/

Um Pouco Mais Sobre A Historia

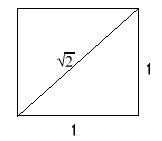
Matemáticas, um dos primeiros irracionais está diretamente ligado ao Teorema de Pitágoras, o número √2 (raiz quadrada de dois) surge da aplicação da relação de Pitágoras no triângulo retângulo com catetos medindo 1 (uma) unidade.

Nessa época, o conhecimento permitia extrair somente a raiz de números que possuíam quadrados inteiros, por exemplo, 4² = 16, portando √16 = 4 e no caso de √2 não existia um número que, elevado ao quadrado, resultasse 2.
Outro irracional surgiu da relação entre o comprimento da circunferência e o seu diâmetro, resultando um número constante igual a 3,141592....., representado pela letra grega π (lê-se pi). O número de Ouro também é considerado irracional, através de pesquisas e observações o Matemático Leonardo de Pisa, mais conhecido como Fibonacci, estabeleceu a seguinte sequência numérica: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .... Essa sequência é formada obedecendo a uma montagem lógica, observe:

1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55

Note que o próximo número da sequência é formado através da soma entre o atual e seu sucessor. Nessa sequência numérica, o número irracional surge da divisão entre um elemento e seu antecessor, a partir do número 21, veja:

5 : 3 = 1,666666.....
8 : 5 = 1,6
13 : 8 = 1,625
21 : 13 = 1,6153846153846153846153846153846 ...
34 : 21 = 1,6190476190476190476190476190476 ...
55: 34 = 1,6176470588235294117647058823529 ...

John Napier, matemático que intensificou os estudos sobre logaritmos, desenvolveu uma expressão que, ao ser calculada, resulta em um número irracional:

O número irracional não admite representação na forma de fração (contrário dos números racionais) e também quando escrito na forma de decimal é um número infinito e não periódico.

Exemplos

π = 3,141592653589793238462... no número pi, após a virgula, não existe formação de períodos, por isso é considerado irracional.

0,232355525447... é infinito e não é dízima periódica (pois os algarismos depois da vírgula não formam períodos), então é irracional.

2,102030569... não admite representação fracionária, pois não é dízima periódica.

Se utilizarmos uma calculadora veremos que √2 , √3 , √5, √7, entre outros, são valores que representam números irracionais.

A representação do conjunto dos irracionais é feita pela letra I maiúscula.

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Fonte:  http://www.brasilescola.com/matematica/numeros-irracionais.htm

DayaneRocha.

"Ao longo do tempo muitos homens conseguiram atingir o êxtase da criação. A estes homens dá-se o nome de MATEMÁTICOS." (autor desconhecido)

Sabrina

Historia

Os primeiros indícios relacionados ao conceito de número irracional remontam ao conceito de incomensurabilidade. Dois segmentos são comensuráveis se existe uma unidade comum na qual podem ser medidos de forma exata. Por exemplo, um segmento de medida e outro de medida podem ser expressos por múltiplos inteiros de um segmento de medida , ou seja, e .

A primeira descoberta de um número irracional é geralmente atribuída a Hipaso de Metaponto, um seguidor de Pitágoras. Ele teria produzido uma demonstração (provavelmente geométrica) de que a raiz de 2 (ou talvez que o número de ouro) é irracional. No entanto, Pitágoras considerava que a raiz de 2 "maculava" a perfeição dos números, e portanto não poderia existir. Mas ele não conseguiu refutar os argumentos de Hipaso com a lógica, e a lenda diz que Pitágoras condenou seu seguidor ao afogamento.

A partir daí os números irracionais entraram na obscuridade, e foi só com Eudoxo de Cnido que eles voltaram a ser estudados pelos gregos. O décimo livro da série Os elementos de Euclides é dedicado à classificação de números irracionais.

Foi só em 1872 que o matemático alemão Dedekind (de 1831 a 1916) fez entrar na Aritmética, em termos rigorosos, os números irracionais que a geometria sugerira havia mais de vinte séculos.

Fonte: http://pt.wikipedia.org/wiki/N%C3%BAmero_irracional
DayaneRocha.

Número irracional é um número real que não pode ser obtido pela divisão de dois números inteiros, ou seja, são números reais mas não racionais. O conjunto dos números irracionais é representado pelo símbolo.
Os números irracionais são representados pela letra I (maiúscula). Estes números não admitem serem escritos na forma de fração, pois em suas formas decimais, consistem em números infinitos não periódicos. 

 

Dayane / Leticia. 

1. Fonte: http://pt.wikipedia.org/wiki/N%C3%BAmero_irracional